Studying Stiffness Equation Assembly and Solution

Displaying the stiffness matrix in non-frontal form

The non-frontal form here implies all assembly forms except frontal form. Thus, full square matrix form, upper-triangular form, band matrix form and skyline form belong to this category. One commonality of these assembly methods is that the whole stiffness matrix is assembled completely in the main memory prior to elimination process. Second commonality is that the assembly and the elimination process is separated.

< Non-frontal assembly forms >

If the popup menu is set to "Square Matrix" item, the stiffness matrix is displayed in square matrix form. The symmetric nature of the matrix appears on the display. In actual programs, the stiffness matrix is seldom assembled in square matrix form. However, this option is provided for educational purposes so that the user may explore the characteristics of the stiffness matrix. The matrix includes entries associated with all d.o.f., and is initially not partitioned.

Displaying the matrix in upper triangular matrix form

If the popup menu is set to “Symmetric Sqr. Matrix” item, the stiffness matrix is displayed in upper triangular form. This form of matrix assembly is meaningful on the assumption that the entries in the upper triangle of the matrix are assembled in one dimensional array. The form is seldom used in an actual program, but is also provided for educational purposes only.

Displaying the matrix in band matrix form

If the popup menu is set to “ Band Matrix” item, the stiffness matrix is displayed in band matrix form. The band matrix assembly takes advantage of symmetry and sparseness of the matrix. The entries within the half band width from the diagonal are assembled in a 2-dimensional array as illustrated in the following figure.

< Band matrix assembly >

Displaying the matrix in skyline form

If the popup menu is set to “Skyline” item, the stiffness matrix is displayed in skyline form. The entries are assembled in one “dimensional array in reality, but are displayed within the square box due to limited screen space.

< Skyline assembly >

Comparing upper triangular matrix and skyline form

If the popup menu is set to “Symmetric + Skyline” item, the stiffness matrix is displayed in both upper triangular form and skyline form side by side. Click an entry either in upper triangle or in skyline assembly. The matching positions in both forms are highlighted in red color. Thus, the position of an entry can be compared in the two assembly forms.

Partitioning the matrix

Matrix partitioning implies grouping the constrained d.o.f. and the free d.o.f. Conceptually, the stiffness matrix is partitioned prior to assembly, and each partition of the matrix is assembled separately. The partitioned equations can be written as

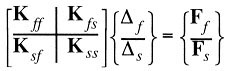
where the subscript f represents free d.o.f., and s represents the constrained d.o.f. The matrix is displayed initially in unpartitioned state. In order to partition stiffness matrix, press “Partition matrix” button . The force vector is also partitioned in accordance with the stiffness matrix. The partitioned and unpartitioned state of the matrix is toggled by clicking the button.

Comparing the required memory of different assembly forms

The required memory for the stiffness matrix is shown as text with the label “Memory space” at the top of “Stiffness Matrix” window. This text changes when the assembly method is altered.

< Memory requirement for matrix assembly >

Examining the effect of node number optimization

In case the stiffness matrix is assembled in non-frontal form, the required memory and the computing time for solution are significantly affected by the node numbering. Thus, it is desirable to optimize the node numbering prior to solving the system equations. The effect of the node number optimization can be identified by noticing the reduced band width of the stiffness matrix. Choose "Optimize Node No.” item from menu. Then, the node number optimization is processed, and the band widths before and after optimization are displayed. At the same time, the stiffness matrix is updated in accordance with the new node numbering. This shows the reduced band width of the stiffness matrix.

Animating the process of matrix assembly

The process of matrix assembly can be graphically visualized by animation. Click "Play" button to start animation. At the beginning of the animation, the global stiffness matrix is cleared. The animation displays the global stiffness matrix progressively being assembled with element stiffness matrices. While animation is going on, the following should be noticed on the mesh drawn in the main window:

At the same time, the following should be noticed on the global stiffness matrix image:

	Only the assembled entries are displayed.
	The numerical value of each entry does not represent the final value, but the value actually assembled so far.
	The entries of the most recently assembled element are marked in red. In order to pause the animation, click “Stop” button .

Examining the process of matrix assembly step by step

Animation may progress too fast to closely examine the process of matrix assembly. This drawback may be overcome by proceeding with the assembly process step by step. This step by step assembly may be started from scratch, or in the middle of animation. In order to move the matrix assembly one step forward, click

“Forward” button . The progress of matrix assembly can be visualized by repeating the button click continuously. In order to move the matrix assembly one step backward, click “Backward” button .

While step by step assembly is going on, the assembled element and the assembled matrix are indicated in the same way as in the case of animation

Assembling the system equations by drag-and-drop

In animation or in step-by-step display of the assembly process, the element stiffness matrices are assembled sequentially from No. 1 element in ascending order of element number. But the order of assembly can be set arbitrarily by the user. In order to enable such an assembly, activate the manual assembly mode by a ressing “Manual assembly mode” button . This manual assembly mode is valid for all types of assembly. Under manual assembly mode, the element stiffness matrix and the force vector can be assembled into the system equations in any order as manipulated by the user. The system equations are assembled by drag-and-drop operation in manual assembly mode.

< Assembling the system equations by drag-and-drop operations >

Simulating the process of solving the system equations

After the system equations are assembled, they are solved through decomposition (or Gauss elimination) and back substitution stages. These two stages can be simulated by this software. For decomposition of the equations, they first be partitioned. So, press button if it is not in pressed state. Then, decompose the equations by pressing button, and proceed for back substitution by pressing button . It is recommended to display in text mode for better understanding on how the equations are changing during the solution process.

< Simulating the solution process >