Examining Element Stiffness Matrix

 

Displaying element stiffness information of continuum structures

The stiffness equations of continuum structures can be expressed by the same equations for frames explained in the previous section. However, the procedure of computing the element stiffness matrix of a continuum structure is totally different from that of a frame. Thus, contents of element stiffness information for continuum stru c t u res are diff e rent from those for frames. The stiffness matrix is obtained generally by the following integration:

Where B is the strain-displacement matrix, and E is the constitutive matrix. In actual computation, the integration is evaluated numerically. Numerical integration can be expressed by the following summation equation.

for plane strain and 3-D solid cases, and

for plane stress, axisymmetric, plate bending and shell analysis, where i is the index for each integration point and m is the number of integration points. Bi, Ei,ti , Ji and wi a re respectively strain-displacement matrix, constitutive matrix, thickness, Jacobian determinant and weight of integration at integration point i. They are included in the element stiffness information.

Root level items

The element stiffness information for continuum structure has the following root level items:

  ¡°Geometry¡± : Nodal coordinates and thickness.
  ¡°Property¡± : Modulus of elasticity, poisson' ratio and constitutive matrix.
  ¡°Integration scheme¡± : Position and weight of each integration point.
  ¡°Shape function and Jacobian matrix¡± : Shape functions, shape function derivatives, Jacobian matrix, its inverse and Jacobian determinant at each integration point.
  ¡°Strain displacement matrix¡± : The strain-displacement matrix computed at each integration point.
  ¡°Stiffness integration¡± : The numerical integration at each integration point.
  ¡°Stiffness matrix¡± : The stiffness matrix obtained by summing the integration at all integration points.

Geometry

Geometry includes the information on the position of each node, and thickness of the element if applicable.

  ¡°Coordinates¡± : The XYZ cartesian coordinates of each node within the element.
  - Node 1 : The coordinates of node 1 of the element .
  - Node n : The coordinates of node n of the element .
 
 
  ¡°Section and length¡± : Thickness of the element. This item is valid only for plane stress, axisymmetric, plate bending and shell analysis (t).

Propert

The element property is defined by 2 elastic constants: modulus of elasticity and Poisson's ratio. The constitutive matrix is determined from these constants.

  ¡±Elastic modulus¡± : Young¡¯s modulus of elasticity applied to all the integration points within the element .
  ¡°Poisson¡¯s ratio¡± : Poisson¡¯s ratio applied to all the integration points within the element .
  ¡°Stress-strain matrix¡± : Constitutive matrix determined by the elastic modulus and Poisson¡¯s ratio.

Integration scheme

There is a sub-item for each integration point. A sub-item has the following information:

 

¡°Weight¡± : The weight of numerical integration for the corresponding integration point. (w)
  ¡°Natural coordinates¡± : The natural coordinates of the integration point. They may be intrinsic natural coordinates, area coordinates, or volume coordinates depending on the element shape and analysis subject. (r, s, t)
  ¡°Cartesian coordinates¡± : The position of the integration point represented in Cartesian coordinates. (X, Y, Z)

< Position of integration points in Cartesian and natural coordinates>

Shape function and Jacobian matrix

Shape function and Jacobian matrix form a sub-item for each integration point. A sub-item has the following information:

 

¡°Shape function¡± : This item displays the shape function of each node evaluated at the integration point, [ N1, N2, ..., Nn. ]
 

¡°Shape function derivative (natural)¡± : The shape function derivatives with respect to the natural coordinates r, s, or t. In case of plane stress, for example,
 

¡°Shape function derivative (Cartesian)": The shape function derivatives with respect to the Cartesian coordinates X, Y, or Z. In case of plane stress, for example,
 

¡°Jacobian matrix¡± : Jacobian matrix, J, transforming the derivatives with respect to Cartesian coordinates to those with respect to natural coordinates. In the case of plane stress, for example,

 
  ¡°Jacobian inverse¡± : Inverse matrix of Jacobian matrix, J-1.
 

¡°Jacobian determinant¡± : Determinant of Jacobian matrix, J =|J|.

Strain-displacement matrix

This is the matrix relating the strain at each integration point to the nodal displacements. The relation between strain and nodal displacements at integration point i is expressed by the equation,

where e, Bi and De are strain vector at integration point i, strain-displacement matrix and nodal displacement vector. In the case of plane stress, for example,

 
 

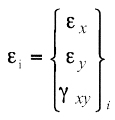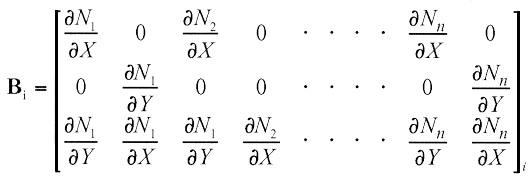and

 

Stiffness integration

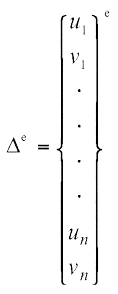This item displays the portion of the numerical integration of the element stiffness matrix at integration point i. The matrix is evaluated at integration point i by the following equation.

for plane strain and 3-D solid cases, and for plane stress, axisymmetric, plate bending and shell analysis.

Stiffness matrix

This item displays the element stiffness matrix obtained by numerical integration.

The element stiffness matrix can be expressed in generic form as follows:

where n is the number of d.o.f. within the element.